Correlation analysis is the important statistical procedure to investigate the relation among the variables. This ultimate guide covers different correlation coefficients and tests for their significance. Find out how to apply correlation analysis in R.
In this guide, we will work on 16 different correlation coefficients in R. These correlation coefficients are available in correlation R package (Makowski et al., 2019). These coefficients are listed below.
- Pearson’s correlation
- Spearman’s rank correlation
- Kendall’s rank correlation
- Biweight midcorrelation
- Distance correlation
- Percentage bend correlation
- Shepherd’s Pi correlation
- Blomqvist’s coefficient
- Hoeffding’s D
- Somers’ D
- Point-Biserial and biserial correlation
- Gamma correlation
- Winsorized correlation
- Gaussian rank Correlation
- Polychoric correlation
- Tetrachoric correlation
We will use correlation() function available in correlation R package (Makowski et al., 2019). There exists method argument in correlation() function. It can be set to one of the correlation coefficients; “pearson” (default), “spearman”, “kendall”, “biweight”, “distance”, “percentage”, “shepherd”, “blomqvist”, “hoeffding”, “somers”, “biserial”, “gamma”, “gaussian”, “polychoric”, “tetrachoric”. Also, there exists adjustment of p-values. If you do not want to make adjustment for p-values, you need to set p_adjust argument to “none”. In this tutorial, we include Pearson’s correlation, Spearman’s rank correlation and biweight midcorrelation. The use of other methods and more detailed information regarding these methods for correlation analysis can be found here.
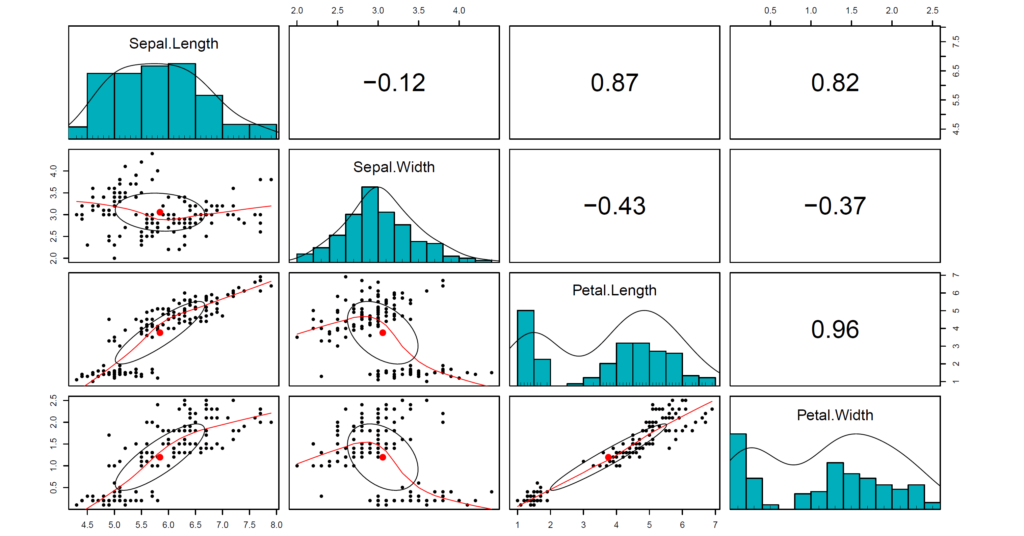
In this part, we will use iris data set available in R. Firstly, we will learn how to apply Pearson method for correlation analysis. Secondly, we will go over Spearman correlation coeffient – equal to the Pearson correlation between the rank values of those two variables. Thirdly, we will learn how to use biweight midcorrelation – robust alternative to Pearson correlation coefficient. Then, we will work on correlation analysis of selected variables. After that, we learn how to rename the selected variables while making corelation analysis. At last, we work on how to obtain correlation matrix.
1) Pearson Method for Correlation Analysis in R
In this part, Pearson correlation coefficients, their confidence intervals and tests for their significance are obtained via correlation() function by setting method = “pearson”.
library(correlation)
correlation(iris, method = "pearson", p_adjust = "none")
## Correlation Matrix (pearson-method)
##
## Parameter1 | Parameter2 | r | 95% CI | t(148) | p
## -------------------------------------------------------------------------
## Sepal.Length | Sepal.Width | -0.12 | [-0.27, 0.04] | -1.44 | 0.152
## Sepal.Length | Petal.Length | 0.87 | [ 0.83, 0.91] | 21.65 | < .001***
## Sepal.Length | Petal.Width | 0.82 | [ 0.76, 0.86] | 17.30 | < .001***
## Sepal.Width | Petal.Length | -0.43 | [-0.55, -0.29] | -5.77 | < .001***
## Sepal.Width | Petal.Width | -0.37 | [-0.50, -0.22] | -4.79 | < .001***
## Petal.Length | Petal.Width | 0.96 | [ 0.95, 0.97] | 43.39 | < .001***
##
## p-value adjustment method: none
## Observations: 150
Check Out: How to Clean Data in R
2) Spearman Method for Correlation Analysis in R
In this section, Spearman correlation coefficients, their confidence intervals and tests for their significance are obtained via correlation() function by setting method = “spearman”.
library(correlation)
correlation(iris, method = "spearman", p_adjust = "none")
## Correlation Matrix (spearman-method)
##
## Parameter1 | Parameter2 | rho | 95% CI | S | p
## ---------------------------------------------------------------------------
## Sepal.Length | Sepal.Width | -0.17 | [-0.32, 0.00] | 6.56e+05 | 0.041*
## Sepal.Length | Petal.Length | 0.88 | [ 0.84, 0.91] | 66429.35 | < .001***
## Sepal.Length | Petal.Width | 0.83 | [ 0.78, 0.88] | 93208.42 | < .001***
## Sepal.Width | Petal.Length | -0.31 | [-0.45, -0.15] | 7.37e+05 | < .001***
## Sepal.Width | Petal.Width | -0.29 | [-0.43, -0.13] | 7.25e+05 | < .001***
## Petal.Length | Petal.Width | 0.94 | [ 0.91, 0.95] | 35060.85 | < .001***
##
## p-value adjustment method: none
## Observations: 150
Also Check: How to Handle Missing Values in R
3) Biweight Midcorrelation Method for Correlation Analysis in R
In this part, biweight midcorrelation coefficients, their confidence intervals and tests for their significance are obtained via correlation() function by setting method = “biweight”.
library(correlation)
correlation(iris, method = "biweight", p_adjust = "none")
## Correlation Matrix (biweight-method)
##
## Parameter1 | Parameter2 | r | 95% CI | t(148) | p
## -------------------------------------------------------------------------
## Sepal.Length | Sepal.Width | -0.13 | [-0.29, 0.03] | -1.65 | 0.100
## Sepal.Length | Petal.Length | 0.83 | [ 0.78, 0.88] | 18.24 | < .001***
## Sepal.Length | Petal.Width | 0.82 | [ 0.76, 0.87] | 17.34 | < .001***
## Sepal.Width | Petal.Length | -0.43 | [-0.55, -0.29] | -5.80 | < .001***
## Sepal.Width | Petal.Width | -0.37 | [-0.50, -0.23] | -4.91 | < .001***
## Petal.Length | Petal.Width | 0.95 | [ 0.93, 0.97] | 37.96 | < .001***
##
## p-value adjustment method: none
## Observations: 150
Also Check: One-way ANOVA for Non-normal and Non-homogeneous Data with Box-Cox Transformation in R
4) Correlation Analysis of Selected Variables in R
The desired variables can be selected in select argument. Here, we select sepal length and sepal width.
library(correlation)
correlation(iris, method = "pearson", select = c("Sepal.Length", "Sepal.Width"), p_adjust = "none")
## Correlation Matrix (pearson-method)
##
## Parameter1 | Parameter2 | r | 95% CI | t(148) | p
## -------------------------------------------------------------------
## Sepal.Length | Sepal.Width | -0.12 | [-0.27, 0.04] | -1.44 | 0.152
##
## p-value adjustment method: none
## Observations: 150
5) How to Rename Selected Variables in Correlation Analysis
We can also rename the selected variables while making corelation analysis with correlation() function. For this purpose, we use rename argument.
library(correlation)
correlation(iris, select = c("Sepal.Length", "Sepal.Width"), rename = c("Sepal Length", "Sepal Width"), p_adjust = "none")
## Correlation Matrix (pearson-method)
##
## Parameter1 | Parameter2 | r | 95% CI | t(148) | p
## -------------------------------------------------------------------
## Sepal Length | Sepal Width | -0.12 | [-0.27, 0.04] | -1.44 | 0.152
##
## p-value adjustment method: none
## Observations: 150
6) How to Obtain Correlation Matrix in R
In this part, we obtain correlation matrix using summary() function.
library(correlation)
out <- correlation(iris, method = "pearson", p_adjust = "none")
summary(out)
## Correlation Matrix (pearson-method)
##
## Parameter | Petal.Width | Petal.Length | Sepal.Width
## -------------------------------------------------------
## Sepal.Length | 0.82*** | 0.87*** | -0.12
## Sepal.Width | -0.37*** | -0.43*** |
## Petal.Length | 0.96*** | |
summary(out, redundant = TRUE)
## Correlation Matrix (pearson-method)
##
## Parameter | Sepal.Length | Sepal.Width | Petal.Length | Petal.Width
## ----------------------------------------------------------------------
## Sepal.Length | 1.00*** | -0.12 | 0.87*** | 0.82***
## Sepal.Width | -0.12 | 1.00*** | -0.43*** | -0.37***
## Petal.Length | 0.87*** | -0.43*** | 1.00*** | 0.96***
## Petal.Width | 0.82*** | -0.37*** | 0.96*** | 1.00***
The application of the codes is available in our youtube channel below.
Don’t forget to check: Heteroscedastic ANOVA Tests in R
References
Makowski, D., Ben-Shachar, M. S., Patil, I., & Lüdecke, D. (2019). Methods and Algorithms for Correlation Analysis in R. Journal of Open Source Software, 5(51), 2306.

Leave a Reply