Variance Homogeneity Tests in R

Variance homogeneity is one of the most certain assumptions for parametric hypothesis tests. This inclusive guide covers the tests of variance homogeneity. Find out how to check variance homogeneity in R.

In this guide, we will work on three tests of variance homogeneity in R.

• Bartlett’s test: Data need to be normally distributed.
• Levene’s test: Less sensitive to departures from normality.
• Fligner-Killeen test: Very robust against departures from normality.

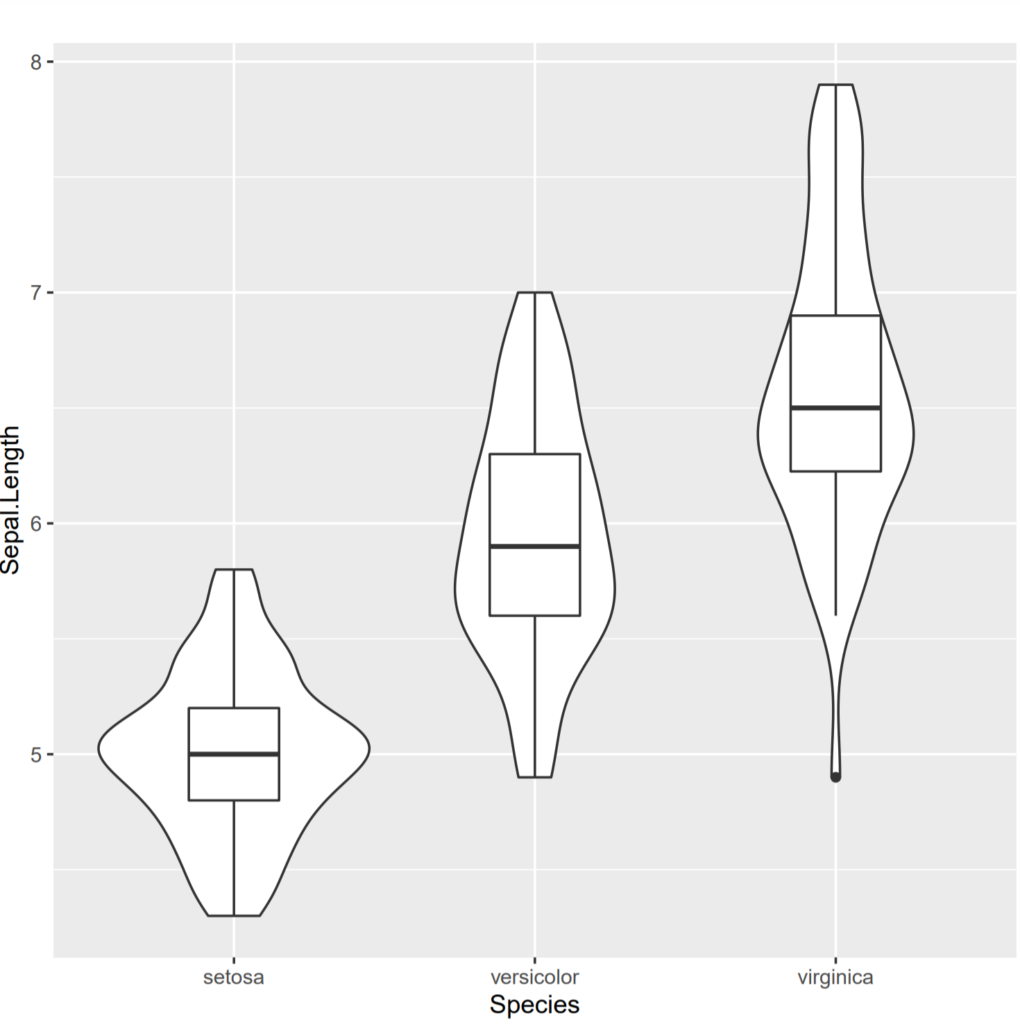
We will use homog.test() function available in onewaytests package (Dag et al., 2018) in R. In this part, we will check variance homogeneity of sepal length among iris types (setosa, virginica, versicolor) as an example data. Before we start, we draw box-and-whisker plot with violin line for visual assessment.

library(onewaytests)
gplot(Sepal.Length ~ Species, data = iris, type = "boxplot")

Check Out: Shapiro-Wilk Test for Univariate and Multivariate Normality in R

1. Bartlett’s Homogeneity Test in R

In this section, we work on Bartlett’s homogeneity test in R. We use homog.test() function available onewaytests package (Dag et al., 2018). We need to set method argument to “Bartlett”.

library(onewaytests)
homog.test(Sepal.Length ~ Species, data = iris, method = "Bartlett")
## 
##   Bartlett's Homogeneity Test (alpha = 0.05) 
## ----------------------------------------------- 
##   data : Sepal.Length and Species 
## 
##   statistic  : 16.0057 
##   parameter  : 2 
##   p.value    : 0.0003345076 
## 
##   Result     : Variances are not homogeneous. 
## ----------------------------------------------- 

According to the result of Bartlett’s homogeneity test, there is enough evidence to reject null hypothesis (Ho: Variances are homogeneous) since p-value (0.0003345076) is lower than alpha (0.05). Therefore, the variances among iris species are not homogeneous.

Also Check: How to Assess Normality in R

2. Levene’s Homogeneity Test in R

In this part, we need to set method argument to “Levene” in homog.test() function available onewaytests package (Dag et al., 2018).

library(onewaytests)
homog.test(Sepal.Length ~ Species, data = iris, method = "Levene")
## 
##   Levene's Homogeneity Test (alpha = 0.05) 
## ----------------------------------------------- 
##   data : Sepal.Length and Species 
## 
##   statistic  : 7.381092 
##   num df     : 2 
##   denum df   : 147 
##   p.value    : 0.0008817888 
## 
##   Result     : Variances are not homogeneous. 
## ----------------------------------------------- 

According to Levene’s homogeneity test, there is enough evidence to reject null hypothesis (Ho: Variances are homogeneous) since p-value (0.0008817888) is lower than alpha (0.05). Therefore, the variances among groups are not homogeneous.

Also Check: How to Recode Character Variables in R

3. Fligner-Killeen Homogeneity Test in R

In this section, we work on Fligner-Killeen homogeneity test in R. We use homog.test() function available onewaytests package (Dag et al., 2018). We need to set method argument to “Fligner”.

library(onewaytests)
homog.test(Sepal.Length ~ Species, data = iris, method = "Fligner")
## 
##   Fligner-Killeen Homogeneity Test (alpha = 0.05) 
## --------------------------------------------------- 
##   data : Sepal.Length and Species 
## 
##   statistic  : 11.61798 
##   parameter  : 2 
##   p.value    : 0.003000458 
## 
##   Result     : Variances are not homogeneous. 
## ---------------------------------------------------

According to Fligner-Killeen homogeneity test, there is enough evidence to reject null hypothesis (Ho: Variances are homogeneous) since p-value (0.003000458) is lower than alpha (0.05). Therefore, the variances among groups are not homogeneous.

The application of the codes is available in our youtube channel below.

Don’t forget to check: How to Categorize Numeric Variables in R

References

Dag, O., Dolgun, A., Konar, N.M. (2018). onewaytests: An R Package for One-Way Tests in Independent Groups Designs. R Journal, 10(1), 175-199.

---

• LinkedIn
• Twitter
• Mail

---